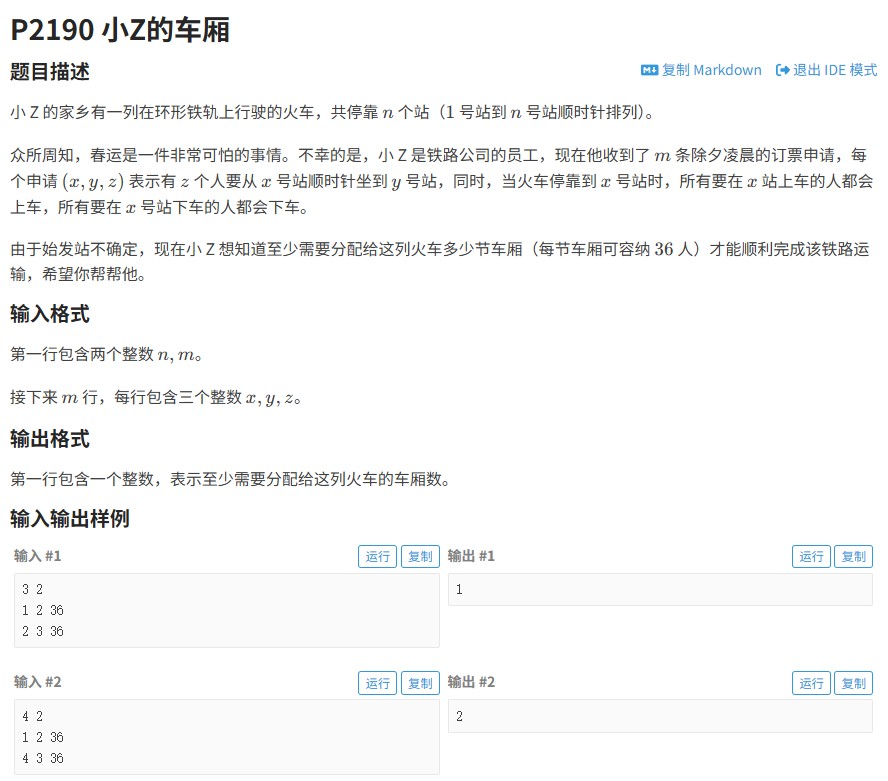
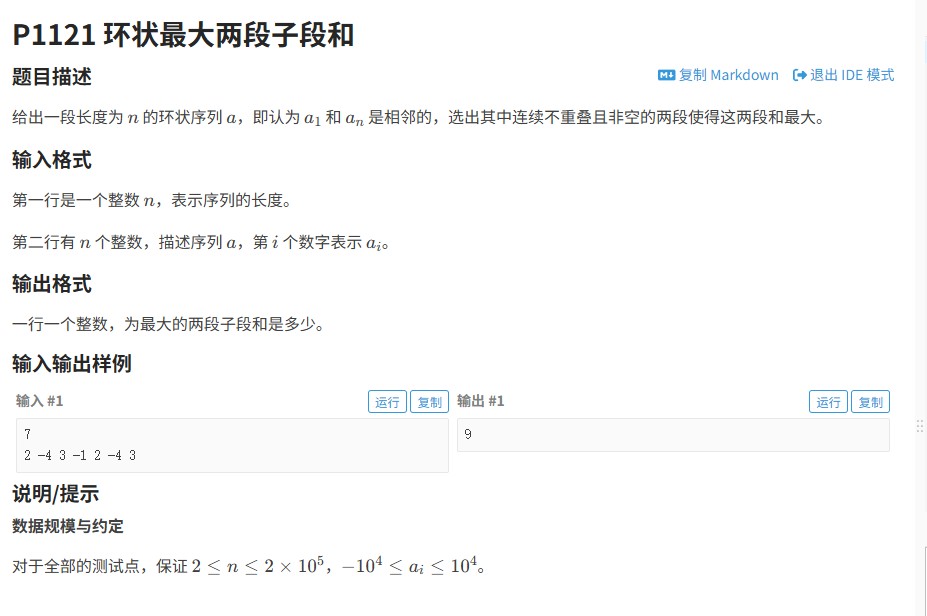
力扣965题深度解析：单值二叉树的判断技巧

重新解读题目 

判断一棵二叉树是否为“单值二叉树”，即所有节点的值是否完全相同。题目看似简单，实则考验对树结构递归特性的理解。若一棵树的所有节点值相同，其必然满足：根节点与左右子树的值一致，且左右子树各自也为单值二叉树。这一特性，为递归解法提供了清晰的切入点。

解题思路与过程 

用递归分治策略，将大问题拆解为小问题：若一棵树是单值二叉树，其左右子树必须同样是单值二叉树，且所有子节点的值与根节点相等。

1. 边界条件：当树为空或仅含根节点时，直接返回true（空树视为单值，单个节点自然满足）。

2. 递归判定： 

        递归调用左、右子树，判断其是否为单值树（LAndR变量）。 

        若左右子树均合法，进一步检查根节点与左右子节点的值是否一致（RootAndLAndR变量）。 

        通过逻辑与（LAndR && RootAndLAndR）综合子树结果与根节点关系，最终返回结论。 

带注释的代码解析

class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        // 空树或仅含根节点，直接返回true
        if (!root || (!root->left &&!root->right))  
            return true;  
        
        // 递归判断左右子树是否为单值树
        bool LAndR = isUnivalTree(root->left) && isUnivalTree(root->right);  
        // 判断根节点与左右子节点是否值相同
        bool RootAndLAndR = true;  
        if (root->left && root->right)  
            RootAndLAndR = (root->val == root->left->val && root->val == root->right->val);  
        else if (root->left)  
            RootAndLAndR = (root->val == root->left->val);  
        else  
            RootAndLAndR = (root->val == root->right->val);  
        
        // 综合子树结果与根节点关系
        return LAndR && RootAndLAndR;  
    }
};

参考：力扣965题 解题思路和步骤 C++代码实现,力扣题库答案在哪里