力扣LCR074题区间合并算法解析:贪心排序与区间重叠处理

一、题目解读
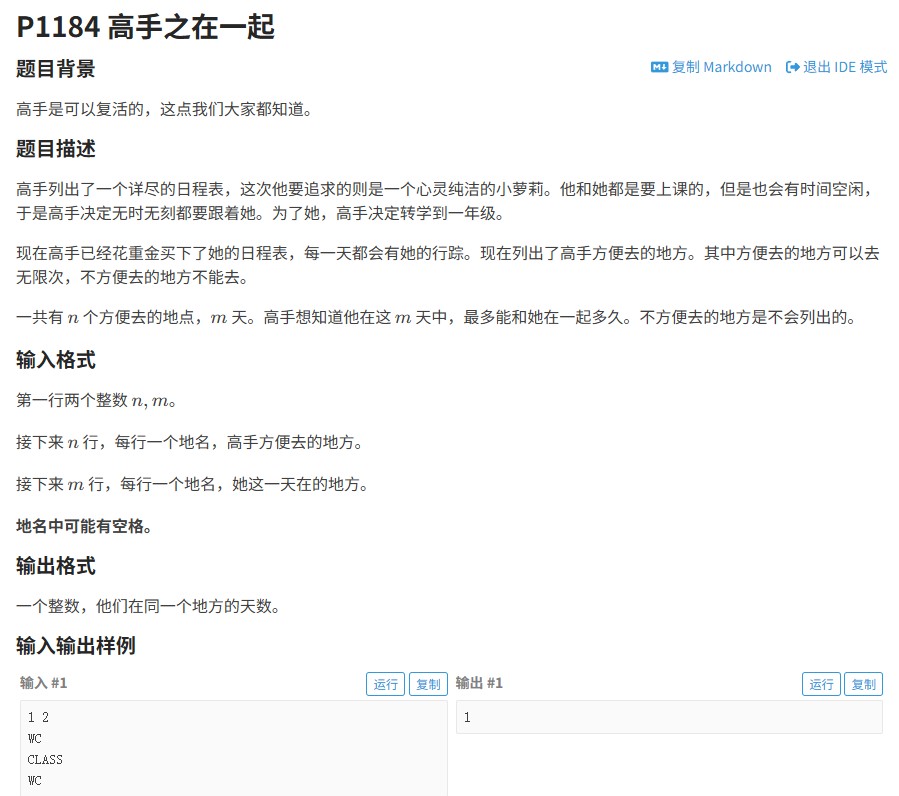
力扣LCR074题要求对给定的二维区间数组(每个区间由起始点和终止点构成)进行合并,将重叠的区间合并为更宽的区间,最终输出不重叠的合并结果。例如,输入[[1,3],[2,6],[8,10],[15,18]],输出[[1,6],[8,10],[15,18]]。核心在于判断区间重叠逻辑与合并策略。
二、解题思路
1. 先排序:按区间起始点升序排列,确保后续遍历时能自然判断相邻区间的重叠关系。
2. 再合并:遍历排序后的区间,通过比较当前区间与末尾合并区间的终止点,决定是否合并或新增区间。
该思路关键在于利用排序减少遍历时的决策复杂度,符合贪心策略的“局部最优解推动全局最优”原则。
三、解题步骤
1. 空数组处理:若输入为空,直接返回空数组,避免后续逻辑错误。
2. 排序区间:使用C++的sort函数配合自定义比较函数(lambda表达式),按区间起始点排序。
3. 初始化合并数组:将第一个区间加入merged数组,作为合并基准。
4. 遍历合并:
○ 从第2个区间开始遍历,每次获取merged末尾区间(last)。
○ 若当前区间起始点≤ last[1](即重叠),则更新last[1]为二者终止点的最大值。
○ 若不重叠,直接添加当前区间至merged。
5. 返回结果:最终merged即为合并后的不重叠区间列表。
四、代码与注释
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.empty()) return {};
// 1. 按照区间起始点排序
sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b) {
return a[0] < b[0];
});
vector<vector<int>> merged;
merged.push_back(intervals[0]);
// 2. 遍历并合并重叠区间
for (int i = 1; i < intervals.size(); ++i) {
// 获取最后一个合并后的区间
vector<int>& last = merged.back();
// 如果当前区间与最后一个合并区间重叠
if (intervals[i][0] <= last[1]) {
// 合并区间,取最大的结束点
last[1] = max(last[1], intervals[i][1]);
} else {
// 不重叠,直接添加新区间
merged.push_back(intervals[i]);
}
}
return merged;
}
};五、总结
该解法时间复杂度为O(nlogn)(排序)+ O(n)(遍历),空间复杂度为O(n)(合并数组)。优点是逻辑简洁、易于实现,缺点是对大规模数据排序可能耗时。实际应用中,若区间数量可控,此贪心排序策略能有效解决重叠合并问题。建议进一步优化可探索不排序的区间树或扫描线算法,但复杂度可能上升。
原创内容 转载请注明出处