牛客25665题详解：二叉树重建与三种遍历实现

一、题目解读

牛客25665题要求根据给定的层序遍历和中序遍历序列重建二叉树，并输出：

    1.所有叶子节点（从左到右）

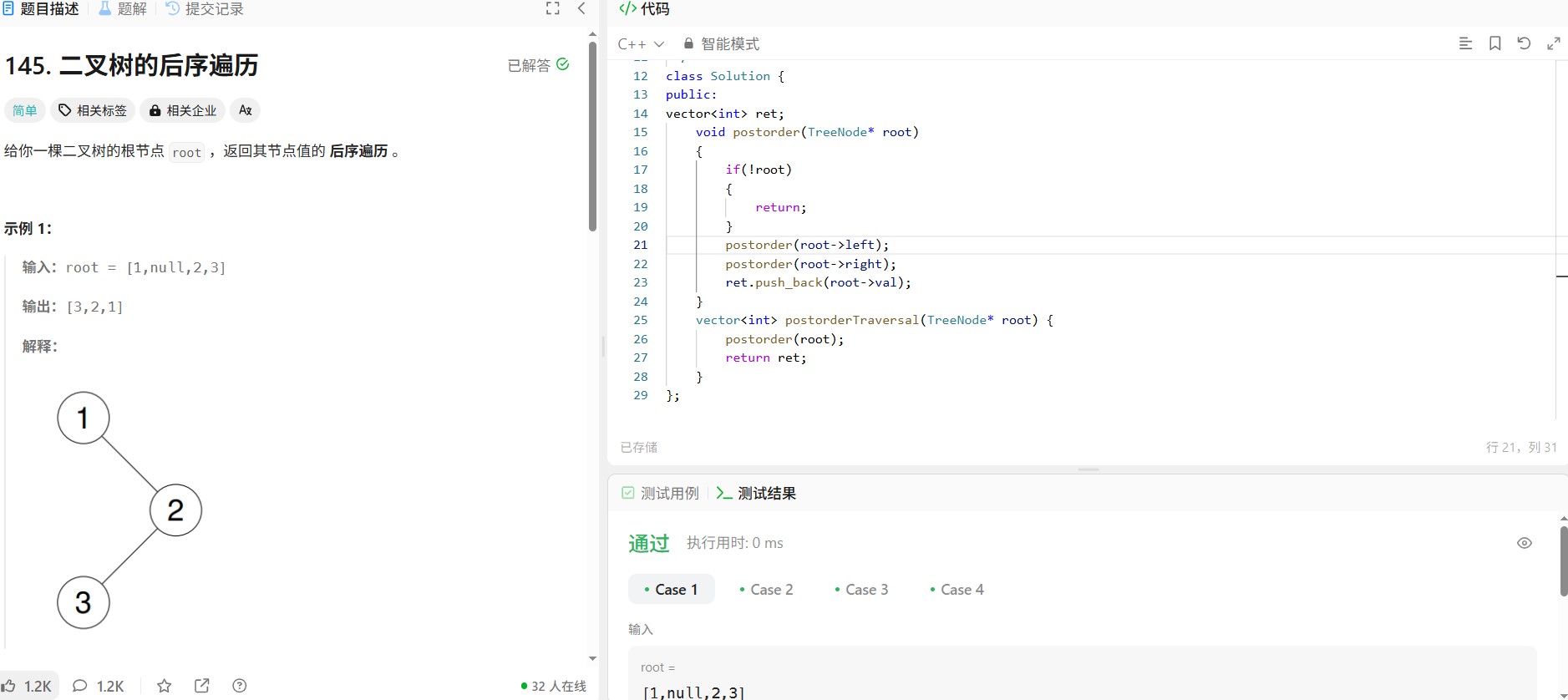
    2.前序遍历序列

    3.后序遍历序列

二、解题思路

1.代码采用分治算法实现：

    使用哈希表记录中序遍历位置

2.递归构建二叉树：

    每次取层序首个元素作为根节点

    根据中序分割左右子树

    筛选层序中属于左/右子树的元素

3.三种遍历实现：

    前序：根→左→右

    后序：左→右→根

    叶子节点：左右子节点均为空

三、解题步骤

1.读取输入数据（层序+中序）

2.建立中序遍历位置索引

3.递归构建二叉树

4.获取叶子节点和前序/后序遍历结果

5.格式化输出结果

四、完整代码实现

#include <iostream>
#include <vector>
#include <unordered_map>
#include <queue>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left, *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

TreeNode* build(vector<int>& level, vector<int>& in, 
               int inStart, int inEnd, unordered_map<int,int>& pos) {
    if (level.empty() || inStart > inEnd) return nullptr;
    
    TreeNode* root = new TreeNode(level[0]);
    int idx = pos[level[0]];
    
    vector<int> leftLevel, rightLevel;
    unordered_map<int,bool> inLeft;
    for (int i = inStart; i < idx; i++) 
        inLeft[in[i]] = true;
    
    for (int i = 1; i < level.size(); i++) {
        if (inLeft.count(level[i])) 
            leftLevel.push_back(level[i]);
        else 
            rightLevel.push_back(level[i]);
    }
    
    root->left = build(leftLevel, in, inStart, idx-1, pos);
    root->right = build(rightLevel, in, idx+1, inEnd, pos);
    return root;
}

void getLeaves(TreeNode* root, vector<int>& res) {
    if (!root) return;
    if (!root->left && !root->right) 
        res.push_back(root->val);
    getLeaves(root->left, res);
    getLeaves(root->right, res);
}

void traversal(TreeNode* root, vector<int>& res, int type) {
    if (!root) return;
    if (type == 1) res.push_back(root->val); // pre
    traversal(root->left, res, type);
    traversal(root->right, res, type);
    if (type == 2) res.push_back(root->val); // post
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    vector<int> level, in;
    string line;
    
    // 读取层序遍历
    getline(cin, line);
    size_t pos = 0;
    while ((pos = line.find(' ')) != string::npos) {
        level.push_back(stoi(line.substr(0, pos)));
        line.erase(0, pos + 1);
    }
    if (!line.empty()) level.push_back(stoi(line));
    
    // 读取中序遍历
    getline(cin, line);
    pos = 0;
    while ((pos = line.find(' ')) != string::npos) {
        in.push_back(stoi(line.substr(0, pos)));
        line.erase(0, pos + 1);
    }
    if (!line.empty()) in.push_back(stoi(line));
    
    // 建立中序位置索引
    unordered_map<int, int> inPos;
    for (int i = 0; i < in.size(); i++) 
        inPos[in[i]] = i;
    
    // 重建二叉树
    TreeNode* root = build(level, in, 0, in.size()-1, inPos);
    
    // 处理输出
    vector<int> leaves, pre, post;
    getLeaves(root, leaves);
    traversal(root, pre, 1);
    traversal(root, post, 2);
    
    // 输出结果
    for (int i = 0; i < leaves.size(); i++) 
        cout << (i ? " " : "") << leaves[i];
    cout << endl;
    
    for (int i = 0; i < pre.size(); i++) 
        cout << (i ? " " : "") << pre[i];
    cout << endl;
    
    for (int i = 0; i < post.size(); i++) 
        cout << (i ? " " : "") << post[i];
    cout << endl;
    
    return 0;
}

五、总结

本文详解了通过层序+中序重建二叉树的算法，实现了三种遍历方式。该解法时间复杂度O(n²)，空间复杂度O(n)，适合笔试面试准备。关键点在于递归分割中序序列和筛选层序子序列。